| Ultimi argomenti attivi | » Frizione Koenigsegg LST, come funziona Sab Mar 28, 2020 9:04 am Da ddefalco » Es. Esame Matlab: Data la matrice A, determinare quale vettore colonna della matrice B appartiene allo spazio colonne della matrice A. Gio Gen 11, 2018 7:56 pm Da SN92 » Molpendolo estensibile  Mar Mag 09, 2017 8:38 pm Da hacknowledge » Decomposizione in valori singolari in Matlab Gio Nov 03, 2016 9:42 pm Da Gianluca93 » LA A^-1 rispetta le 4 proprietà della inversa generalizzata di MP Mer Nov 02, 2016 3:04 pm Da r.mauro » How a differential works? Dom Lug 10, 2016 10:57 am Da Mario95 » Manovellismo di spinta rotativa: Caso manovella disposta a 90° rispetto all'asse di scorrimento del pistone Lun Giu 20, 2016 6:21 am Da ddefalco » QuIRK Multibody Dynamics Esempio pendolo piano Gio Mag 05, 2016 8:37 am Da bestlin » QuIRK Multibody Dynamics Package Sab Mar 12, 2016 4:03 pm Da SN92 |
|
| | Cinematica del manovellismo di spinta rotativo |  |
|
+3limatola.giovanni Feola Michele ddefalco 7 partecipanti | | Autore | Messaggio |
|---|
ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Cinematica del manovellismo di spinta rotativo Titolo: Cinematica del manovellismo di spinta rotativo  Mar Apr 13, 2010 11:38 am Mar Apr 13, 2010 11:38 am | |
|  
Per scaricare le immagini ingrandite cliccare con il tasto dx sull'immagine e poi "salva con nome..."
Potete scaricare i file autocad [cliccando qui]Nelle figure sono riportati, rispettivamente, gli schemi cinematici di un motore monocilindrico e di un motore bicilindrico con cilindri a V di 90°. Per entrambi i meccanismi determinare geometricamente quanto segue: - la posizione di punto morto superiore (PMS) e punto morto inferiore (PMI) di ognuno dei pistoni;
- la configurazione, per ognuno dei meccanismi, nei casi definiti nella seguente tabella
| conf. | Monocilindrico | V2 di 90° | | a | pistone al PMI | pistone 2 (destro) al PMI | | b | manovella ruotata di 30° | manovella ruotata di 30° | | c | manovella ruotata di 60° | manovella ruotata di 105° | | d | pistone al PMS | pistone 2 al PMS |
- le posizioni dei centri di istantanea rotazione assoluti della biella in ognuna delle posizioni del meccanismo definite precedentemente
- le posizioni dei centri di istantanea rotazione della biella relativi alla configurazione d definito nella tabella precedente.
Ultima modifica di ddefalco il Gio Mag 03, 2012 7:58 pm - modificato 1 volta. | |
|   | | Feola Michele
Numero di messaggi : 5
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Feola Michele
Data d'iscrizione : 02.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Mar Apr 13, 2010 8:46 pm Mar Apr 13, 2010 8:46 pm | |
| | |
|   | | limatola.giovanni
Numero di messaggi : 7
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Giovanni Limatola
Data d'iscrizione : 25.02.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Mer Apr 14, 2010 6:46 pm Mer Apr 14, 2010 6:46 pm | |
|  Ho cercato di risolvere l'esercizio per quanto riguarda il manovellismo di spinta rotativo monocilindrico. Nella prima parte (quella superiore) sono mostrate le quattro configurazioni del manovellismo quando si trova rispettivamente: A) nel PMI B) ruotato di 30° rispetto al PMI C) ruotato di 60° rispetto al PMI D) nel PMS Ho ottenuto le configurazioni facendo ruotare rispettivamente la manovella attorno al suo centro di rotazione (che è sempre lo stesso), la posizione della biella l'ho ottenuta tracciando una circonferenza di raggio pari proprio alla lunghezza della biella, puntando nell'estremo libero della manovella e facendo intersecare la circonferenza con l'asse di rotazione centrale del cilindro. Infine ho ovviamente posizionato il pistone accoppiando il suo centro con l'estremo libero della biella. Nella parte inferiore della figura che ho postato invece sono rappresentati i centri di istantanea rotazione rispettivamente di manovella biella e pistone nelle configurazioni B e C. Li ho trovati utilizzando il teorema di Chasles. Si può notare che mentre C1 (centro di rotazione per la manovella) e C2 (centro istantaneo di rotazione per la biella) sono centri propri, C3 (centro di instantanea rotazione per il pistone) è un centro improprio. Spero di non aver commesso errori molto gravi. | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 5:27 am Gio Apr 15, 2010 5:27 am | |
| La ringrazio e complimenti per l'impegno. - Però per quanto riguarda i centri di istantanea rotazione (CIR) della biella, non ci siamo.
Giustamente ha applicato il th di Chasles, ma a chi ?
Deve applicarlo ai 2 punti estremi della biella (diciamoli B e C risp. di collegamento alla manov e al pist) di cui conosce le traiettorie poiché sono rispettivamente le crf. di centri il punto improprio in direz. ort. all'asse del cilindro e O. Pertanto deve disegnare la normale alla traiett. del pistone (all'asse del cilindro) passante proprio per P e la normale alla traiett. di B (che è la crf di centro O) passante proprio per B.
Tra l'altro, se si ricorda, molto semplicemente queste coincidono con i prolungamenti dei due lati del meccanismo ovvero quello degenerato nel punto C (e quindi la perpendic. all'asse del cilindro) e BC e quindi per trovare il CIR basta trovare le intersezioni tra queste rette.
- Dal punto di vista tipografico va benissimo come ha "compilato" le figure e colorato e ridotto l'immagine. I CIR li aggiunga direttamente ai disegni delle varie posizioni del manovellismo poiché proprio a loro si riferiscono.
- Degli errori che eventualmente fate negli esercizi dovete farne tesoro in questa fase. Servono a farvi riflettere, a fare esperienza e la loro pubblicazione è altrettanto utile agli altri. Però dovete capirne bene la causa che, nella maggior parte dei casi, è dovuta ad una lettura non attenta del libro o degli appunti. Ravviso spesso questo problema: i ragazzi credono che risolvere gli esercizi sia una prova di comprensione: non è così !!! Ad es. pensi all' uso del th. di Chasles che ha evocato nel suo ultimo intervento...
Saluti.  | |
|   | | kayman
Numero di messaggi : 2
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Daniele Caimano
Data d'iscrizione : 17.03.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 4:10 pm Gio Apr 15, 2010 4:10 pm | |
|  [color=#000000] Per la posizione dei CIR del piede e della testa di biella negli istanti sopra considerati ho applicato il teorema di Chasles. Il pistone e il piede di biella hanno in ogni istante la direzione della velocità coincidente con l’asse del cilindro per cui ho tracciato la normale (N2)all’asse del cilindro, ovviamente in corrispondenza del collegamento pistone-piede di biella. Invece la testa di biella che è collegata alla manovella, ha la direzione della velocità tangente alla circonferenza che descrive la manovella durante la sua rotazione intorno al proprio centro. Per cui ho tracciato la normale (N2) nei 4 istanti e trovato il CIR attraverso l’intersezione con l’altra retta (N1).Vediamo che nei casi a) e d) il CIR si trova in corrispondenza del collegamento pistone-piede di biella mentre nei casi b) e c) si trova nel centro intorno a cui ruota la manovella. Spero di non aver commesso troppi errori. [/font"> | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 4:43 pm Gio Apr 15, 2010 4:43 pm | |
| Bene, le costruzioni sono corrette nei casi di biella inclinata. Invece qual'è il CIR nei casi di biella e manovella allineate ?
Cio che non mi è chiaro è: al CIR di chi si riferisce ? Insomma cosa vuole dire con "Per la posizione dei CIR del piede e della testa di biella..." ?
Cerchi di rispondere precisamente a queste domande, a parole.
saluti. | |
|   | | Giacomo89
Numero di messaggi : 10
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Giacomo Belgiorno
Data d'iscrizione : 25.02.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 6:11 pm Gio Apr 15, 2010 6:11 pm | |
| 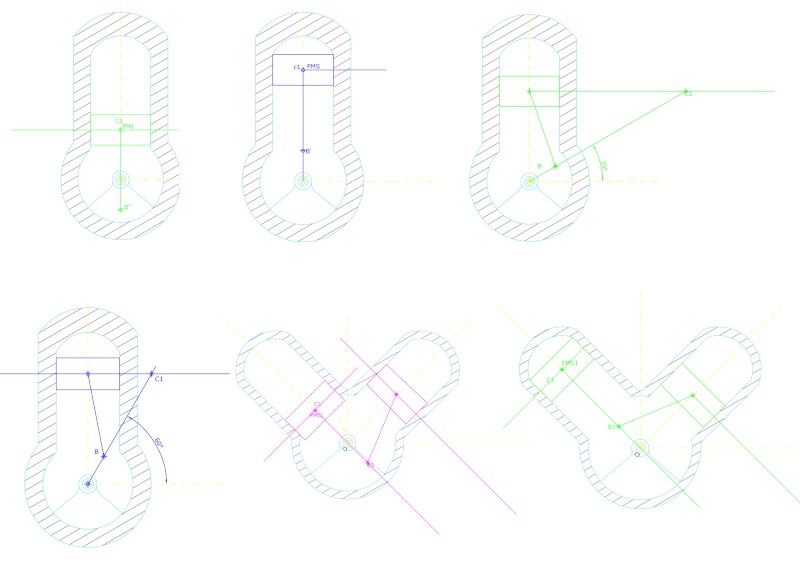 Buonasera a tutti, ho provato anche io a fare l’esercizio proposto, ho analizzato prima lo schema cinematico di un motore monocilindrico, ho tre coppie rotoidali dette O, B, C e una coppia prismatica in quanto il pistone ha un atto di moto rettilineo alternato intorno ad un centro improprio all’infinito nella direzione perpendicolare all’asse del cilindro, la manovella OB ha un atto di moto di rotatorio in un certo istante t intorno ad un centro di rotazione O, mentre per trovare il centro d’istantanea rotazione della biella B C basta applicare il teorema di Chasles note le traiettorie dei punti B e C la prima compie una traiettoria circolare e la seconda una traiettoria rettilinea lungo l’asse, ne faccio le normali alle traiettorie e la loro intersezione ne determina il centro d’istantanea rotazione della biella. Ho trovato il punto morto inferiore del pistone allineando i punti B, O, C tenendo conto che le distanze OB, BC siano le stesse rispetto alla configurazione di partenza, analogamente il punto morto superiore del pistone l’ottengo allineando i punti O, B, C mantendendo fisse le distanze tra di loro. Ho indicato con C1 il centro d’istantanea rotazione della biella quando il pistone si trova nella posizione PMI e con C2 il centro d’istantanea rotazione della biella quando il pistone si trova nella posizione PMS. Buonasera a tutti, ho provato anche io a fare l’esercizio proposto, ho analizzato prima lo schema cinematico di un motore monocilindrico, ho tre coppie rotoidali dette O, B, C e una coppia prismatica in quanto il pistone ha un atto di moto rettilineo alternato intorno ad un centro improprio all’infinito nella direzione perpendicolare all’asse del cilindro, la manovella OB ha un atto di moto di rotatorio in un certo istante t intorno ad un centro di rotazione O, mentre per trovare il centro d’istantanea rotazione della biella B C basta applicare il teorema di Chasles note le traiettorie dei punti B e C la prima compie una traiettoria circolare e la seconda una traiettoria rettilinea lungo l’asse, ne faccio le normali alle traiettorie e la loro intersezione ne determina il centro d’istantanea rotazione della biella. Ho trovato il punto morto inferiore del pistone allineando i punti B, O, C tenendo conto che le distanze OB, BC siano le stesse rispetto alla configurazione di partenza, analogamente il punto morto superiore del pistone l’ottengo allineando i punti O, B, C mantendendo fisse le distanze tra di loro. Ho indicato con C1 il centro d’istantanea rotazione della biella quando il pistone si trova nella posizione PMI e con C2 il centro d’istantanea rotazione della biella quando il pistone si trova nella posizione PMS.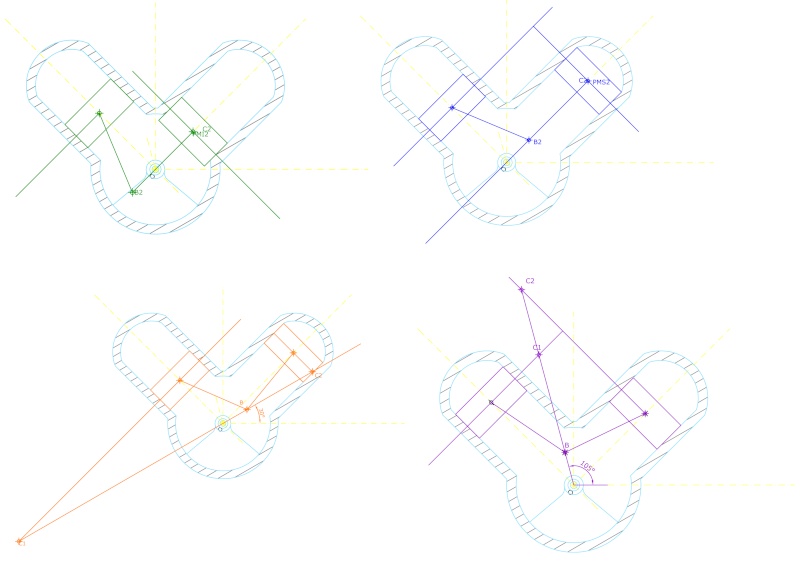 Nello schema cinematico di un motore bicilindrico con cilindri a V di 90° ho individuato le due coppie prismatiche ognuno dei singoli pistone che hanno un atto di moto rettilineo alternato intorno ad un centro improprio all’infinito nella direzione perpendicolare all’asse del cilindro, una coppia rotoidale nel punto O, una coppia rotoidale tra il pistone e la biella (di sinistra), una coppia rotoidale tra il pistone e la biella (di destra)una coppia pismatica tra il cilindro e il pistone di sinistra e un'altra coppia prismatica per il cilindro e il pistone di destra, una coppia rotoidale tra la biella e la manovella (di destra) e una coppia rotoidale tra la biella e la manovella (di sinistra), la manovella ha un atto di moto rotatorio in un certo istante t intorno al centro di rotazione O, i due pistoni hanno un atto di moto traslatorio alternato in un certo instante t intorno a due centri d’istantanea rotazione all’infinito nella direzione perpendicolare alla traiettoria dei pistoni. Per la biella di sinistra quando il pistone di sinistra si trova nella configurazione del PMI note le traiettorie del punto B1 e nota la traiettoria del punto C del pistone ne traccio le normali alle traiettorie e vedo che esse si incontrano proprio nel punto PMI che ho chiamato C1, mentre per la biella di destra il Cr è all’infinito in quanto sia la normale alla traiettoria di B1 e di C del pistone di dx sn parallele tra di loro. Applicando il teorema di Chasles per gli altri casi ho trovati i centri d’istantanea rotazione per le biella di sx e di dx. la posizione dei PMI e PMS è stata trovata come nel caso dello schema del motore monocilindrico sempre considerando fisse le distanze tra i punti OB, BC’ e BC” dove C’ è il punto del pistone di sx e C” è il punto del pistone di dx. Spero di non aver fatto errori gravi. Nello schema cinematico di un motore bicilindrico con cilindri a V di 90° ho individuato le due coppie prismatiche ognuno dei singoli pistone che hanno un atto di moto rettilineo alternato intorno ad un centro improprio all’infinito nella direzione perpendicolare all’asse del cilindro, una coppia rotoidale nel punto O, una coppia rotoidale tra il pistone e la biella (di sinistra), una coppia rotoidale tra il pistone e la biella (di destra)una coppia pismatica tra il cilindro e il pistone di sinistra e un'altra coppia prismatica per il cilindro e il pistone di destra, una coppia rotoidale tra la biella e la manovella (di destra) e una coppia rotoidale tra la biella e la manovella (di sinistra), la manovella ha un atto di moto rotatorio in un certo istante t intorno al centro di rotazione O, i due pistoni hanno un atto di moto traslatorio alternato in un certo instante t intorno a due centri d’istantanea rotazione all’infinito nella direzione perpendicolare alla traiettoria dei pistoni. Per la biella di sinistra quando il pistone di sinistra si trova nella configurazione del PMI note le traiettorie del punto B1 e nota la traiettoria del punto C del pistone ne traccio le normali alle traiettorie e vedo che esse si incontrano proprio nel punto PMI che ho chiamato C1, mentre per la biella di destra il Cr è all’infinito in quanto sia la normale alla traiettoria di B1 e di C del pistone di dx sn parallele tra di loro. Applicando il teorema di Chasles per gli altri casi ho trovati i centri d’istantanea rotazione per le biella di sx e di dx. la posizione dei PMI e PMS è stata trovata come nel caso dello schema del motore monocilindrico sempre considerando fisse le distanze tra i punti OB, BC’ e BC” dove C’ è il punto del pistone di sx e C” è il punto del pistone di dx. Spero di non aver fatto errori gravi. | |
|   | | kayman
Numero di messaggi : 2
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Daniele Caimano
Data d'iscrizione : 17.03.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 7:57 pm Gio Apr 15, 2010 7:57 pm | |
| Allora quando il pistone sta in posizione di PMI e PMS, la direzione della velocità del piede di biella come detto prima non cambia ed è sempre coincidente con l'asse del cilindro e quindi ho rappresentato la sua normale N1 mentre la velocità della testa di biella ha direzione tangente alla circonferenza che descrive la manovella attorno al suo centro di rotazione quindi parallela all'asse x per cui la sua normale N2 ha direzione coincidente con l'asse del cilindro. Le due normali si incontrato proprio nel punto di collegamento tra il pistone e il piede di biella. Questo punto per il torema di chasles rappresenta il CIR della biella. Spero di essere stato chiaro.
Saluti. | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 8:04 pm Gio Apr 15, 2010 8:04 pm | |
| Risposta a Giacomo89:
attenzione: come potrebbe mai essere un atto di moto "rettilineo alternato" ? L'atto di moto è una grandezza che si riferisce ad un certo istante. Ricordate che il rompiscatole pretende che non si dica "atto di moto" bensì "atto di moto ad un certo istante"
Cos'è un atto di moto ad in un certo istante ?
Vorrei che qualcuno SCRIVESSE in un solo rigo cos'è l'atto di moto all'istante t di un sistema... la definizione...
Saluti. | |
|   | | Gabriele Lamberti
Numero di messaggi : 3
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Gabriele Lamberti
Data d'iscrizione : 13.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 8:39 pm Gio Apr 15, 2010 8:39 pm | |
| buonasera professore
si definisce atto di moto ad un certo istante t la distribuzione dei vettori velocità dei punti del sistema ad un fissato istante di tempo (t)
| |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Gio Apr 15, 2010 10:20 pm Gio Apr 15, 2010 10:20 pm | |
| non basta.
L'atto di moto ad un istante t di un sistema è l' INSIEME di vettori APPLICATI costituito dai vettori velocità dei punti del sistema applicati nelle posizioni che tali punti occupano proprio all'istante t.
Eppure ve l'ho data diverse volte questa definizione e c'è sugli appunti: volete mettervi a studiare ?
Allora ha senso dire che "un atto di moto sia rettilineo alternato" ? | |
|   | | Giacomo89
Numero di messaggi : 10
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Giacomo Belgiorno
Data d'iscrizione : 25.02.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Ven Apr 16, 2010 4:17 pm Ven Apr 16, 2010 4:17 pm | |
| Non ha senso parlare di atto di moto rettilineo alternato ma di atto di moto rettilineo alternato in un certo istante t perché in generale non è detto che il sistema abbia vettori velocità dei punti del sistema applicati nelle posizioni che tali punti occupano proprio all'istante t tutti uguali tra di loro, mentre solo se accade che in un certo instante t il sistama abbia i vettori velocità applicati nelle posizioni che tali punti accupano a quell’stante uguali tra di loro allora l’atto di moto è rettilineo alternato in quell’istante pur non essendo il moto rettilineo alternato.
spero di aver capito adesso, e ringrazio per le correzioni sono sempre ben accette. | |
|   | | davide89
Numero di messaggi : 2
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : DavideErcole
Data d'iscrizione : 06.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Dom Apr 18, 2010 11:37 am Dom Apr 18, 2010 11:37 am | |
|   Salve a tutti, sono Davide Ercole. Tento di dare una risposta al quesito 3 Lo scopo è trovare il CIR della Biella nel motore monocilindrico. Ebbene, noi conosciamo le traiettorie di due punti della biella: IL PIEDE DELLA BIELLA (estremità superiore della biella ossia quella collegata al pistone mediante lo spinotto)
LA TESTA DELLA BIELLA (estremità inferiore della biella ossia quella collegata alla manovella)
Ora per quanto riguarda il piede della biella, poiché è vincolata al pistone, ha un moto rettilineo alternato, e quindi all'istante t in cui occupa la posiz. considerata ha atto di moto traslatorio lungo l'asse del cilindro: pertanto per il teorema di Chasles il centro di istantanea rotazione si troverà lungo la normale all'asse del cilindro.
Facendo l'analogo ragionamento per la testa di biella, che è collegata alla manovella, si rileva che esso ha un moto rotatorio intorno al punto O e quindi ha come traiettoria una circonferenza di raggio la lunghezza della manovella. Allora, per il teorema di Chasles la normale alla traiettoria avrà direzione radiale passante per la posizione di B, come in figura.
Pertanto il CIR della biella del motore monocilindrico sarà il punto di intersezione delle due rette tracciate ossia Cb.
Per il motore bicilindrico il ragionamento è analogo, solo che va fatto per una volta per la biella uno (a sinistra) e una volta per la biella 2 (a destra). Così verranno trovati rispettivamente Cb1 e Cb2 che sono i CIR delle bielle.
Non mi è possibile rispondere agli altri quesiti in questo momento perchè ho dei problemi con il CAD infatti i disegni pubblicati sono stati scaricati dal sito e modificati a mano.
Provvederò al più presto a rispondere agli altri quesiti.
Ultima modifica di ddefalco il Dom Apr 18, 2010 3:24 pm - modificato 2 volte. (Motivazione : ho editato una immagine) | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Dom Apr 18, 2010 3:28 pm Dom Apr 18, 2010 3:28 pm | |
| molto bene. La procedura è corretta ed anche la descrizione è precisa e fatta con una terminologia adeguata, indice di un buon grado di comprensione.
Perché non prova a rispondere a questo punto alla domanda:
cosa vuol dire che il CIR della biella si trova in quel punto in quell'istante, sia nel caso del motore monocilindico che in quello del bicilindrico ? | |
|   | | davide89
Numero di messaggi : 2
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : DavideErcole
Data d'iscrizione : 06.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Dom Apr 18, 2010 9:54 pm Dom Apr 18, 2010 9:54 pm | |
| Per questa domanda provo a rispondere in questo modo:
Il moto da noi considerato è un moto rigido piano. ogni moto rigido piano in un certo intervallo di tempo At è costituito da una successione di atti di moti rigidi rotatori dove per ogni istante t cambia il CIR dei punti che subiscono il moto.
Per cui prima di definire un CIR occorre sapere in che istante ci troviamo e per quali punti lo consideriamo (in questo caso i punti della biella, ma anche i punti solidali alla biella)
A questo punto definisco il CIR all'istante t, come il punto di intersezione dell'asse di istantanea rotazione con il piano del moto nell'istante considerato. Esso è importante perchè è possibile esprimere la velocità di tutti i punti di un sistema che si muove di moto rigido piano attraverso la conoscenza del CIR istante per istante, per esempio la velocità di un punto P all'istante t la posso vedere come il prodotto vettoriale tra il vettore (CIR-P) e il vettore w. | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Lun Apr 19, 2010 5:23 am Lun Apr 19, 2010 5:23 am | |
| Perché dice "il moto da noi considerato"? Cosa importa cosa fa la biella in istanti diversi da quello che si sta considerando (la domanda è sull'atto di moto all' istante in cui il meccanismo è nella posizione rappresentata) ? Direi: La biella, nella posizione occupata all'istante di rappresentazione, ha un atto di moto rotatorio di centro di istantanea rotazione CIR e velocità angolare w. Pertanto di ogni suo punto ne conosciamo la velocità, cioè conosciamo la distribuzione delle velocità dei punti della biella, se sappiamo quanto vale la velocità angolare w. Cioé, in conclusione: La distribuzione delle velocità dei punti della biella è: Vp=(CIR-P)^w ovvero Vp è, per ogni punto P della biella, dato dal vettore: normale ad w e quindi è nel piano del motonormale alla congiungente (CIR-P) e di verso tale che la terna {(CIR-P), w, Vp} sia levogira di modulo linearmente dipendente dalla distanza di P da CIR.
 | |
|   | | Gabriele Lamberti
Numero di messaggi : 3
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Gabriele Lamberti
Data d'iscrizione : 13.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Mar Apr 20, 2010 2:07 pm Mar Apr 20, 2010 2:07 pm | |
|  Salve a tutti! Il meccanismo è un sistema rigido ad un grado di libertà quindi, data una coordinata, è possibile trovare le coordinate di tutto il sistema. Ogni elemento del meccanismo ha un centro di istantanea rotazione in quanto il sistema muovendosi di moto rigido, per Mozzi, l’atto di moto è rototraslatorio. Nel nostro caso, poichè ogni elemento dl sistema è piano, le normali delle traiettorie dell’atto di moto ad un certo istante (t), a ogni configurazione sono incidenti in un punto che è il CIR di tutto il sistema (teorema di Chasles) esso, quindi, dipende dalla configurazione del sistema e si riferisce all’istante di posizione. Manovella OB:la manovella non solo ha atto di moto rotatorio ma anche l’intero moto è rotatorio intorno all’ asse di rotazione O che non varia nel tempo di posizione. Così: la normale della traiettoria dell’ atto di moto della manovella è rappresentata da una retta r diretta proprio lungo OB. CIRob=O. Il moto della biella dipende anche dal moto del pistone(rettilineo alternato)collegato ad esso tramite lo spinotto. Dato che il moto del pistone è rigido, per Mozzi, la coppia prismatica di C ha un atto di moto rotatorio ad un punto all’infinito perpendicolare all’asse del pistone r: CIR pist=C∞┴r Collegando, infine, le normali dei link esse si intersecheranno in un punto che è il CIR del sistema il quale permette di ottenere l’atto di moto, in un certo istante t, dell’intero sistema. Mi scuso per eventuali errori e per il disegno, ma non mi è stato ancora possibile procurarmi una versione Autocad, lo farò al più presto possibile. Saluti. | |
|   | | Gabriele Lamberti
Numero di messaggi : 3
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Gabriele Lamberti
Data d'iscrizione : 13.04.10
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Mar Apr 20, 2010 6:29 pm Mar Apr 20, 2010 6:29 pm | |
| *le normali delle traiettorie dei link in un certo istante (t)* | |
|   | | ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  Mer Apr 21, 2010 5:36 am Mer Apr 21, 2010 5:36 am | |
| Riporto delle correzioni all'intervento di Gabriele Lamberti che ritengo molto importanti. Spero ci riflettiate su per bene: | Il meccanismo è un sistema rigido ad un grado di libertà | Il meccanismo non è un sistema rigido (anzi è un sistema articolato)Esso è un sistema di corpi rigidi | | quindi, data una coordinata, è possibile trovare le coordinate di tutto il sistema. | per ogni valore di una coordinata (scelta opportunamente) è individuata la posizione del meccanismo | | Ogni elemento del meccanismo ha un centro di istantanea rotazione in quanto il sistema muovendosi di moto rigido, per Mozzi, l’atto di moto è rototraslatorio. | Ogni elemento del meccanismo ha un centro di istantanea rotazione ognuno di essi, muovendosi di moto rigido, per il th. Mozzi, ha un atto di moto ad ogni istante rototraslatorio. | | Nel nostro caso, poichè ogni elemento del sistema è piano, le normali delle traiettorie dell’atto di moto ad un certo istante (t), a ogni configurazione sono incidenti in un punto che è il CIR di tutto il sistema (teorema di Chasles) esso, quindi, dipende dalla configurazione del sistema e si riferisce all’istante di posizione. | Nel nostro caso, poichè ogni elemento del sistema si muove di moto piano, per ognuno di essi le normali alle traiettorie dei suoi punti in ogni istante ("dell’atto di moto ad un certo istante (t), a ogni configurazione": non ha significato questa frase) sono incidenti in un punto che è il CIR dell'elemento (e non: di tutto il sistema) (teorema di Chasles) esso, quindi, dipende dalla posizione dell'elemento e dalla configurazione del sistema all' istante considerato. | | Manovella OB:la manovella non solo ha atto di moto rotatorio ma anche l’intero moto è rotatorio intorno all’ asse di rotazione O che non varia nel tempo di posizione. Così: la normale della traiettoria dell’ atto di moto della manovella è rappresentata da una retta r diretta proprio lungo OB. CIRob=O. | Manovella OB:la manovella ha atto di moto rotatorio in ogni istante intorno allo stesso centro O e la posizione di questo è fissa (cioè non varia nel tempo) pertanto il moto della manovella è rotatorio intorno al centro di rotazione O. Così: (ma cos'è: la normale della traiettoria dell’ atto di moto della manovella??? )la normale alla traiettoria del punto B appartenente alla manovella è rappresentata da una retta r diretta proprio lungo OB.CIRob=O. | | Il moto della biella dipende anche dal moto del pistone (rettilineo alternato) collegato ad esso tramite lo spinotto. Dato che il moto del pistone è rigido, per Mozzi, la coppia prismatica di C ha un atto di moto rotatorio ad un punto all’infinito perpendicolare all’asse del pistone r: CIR pist=C??r | Il moto della biella dipende anche dal moto del pistone (rettilineo alternato) collegato ad esso tramite lo spinotto. Poiché (Dato che) il moto del pistone è rigido, per il th. di Mozzi, il pistone (la coppia prismatica di C) ha in ogni istante un atto di moto rotatorio intorno ad un punto all’infinito perpendicolare all’asse del pistone r: CIR pist=C??r | | Collegando, infine, le normali dei link esse si intersecheranno in un punto che è il CIR del sistema il quale permette di ottenere l’atto di moto, in un certo istante t, dell’intero sistema. | Tracciando il prolungamento del link rappresentativo della manovella e la perpendicolare all'asse del cilindro passante per la posizione di C (che senso ha la frase: collegando, infine, le normali dei link esse...) si intersecheranno in un punto che è il CIR della biella (non: del sistema) (tutta questa frase: "il quale permette di ottenere l’atto di moto, in un certo istante t, dell’intero sistema" non ha alcun senso). |
| |
|   | | Contenuto sponsorizzato
 |  Titolo: Re: Cinematica del manovellismo di spinta rotativo Titolo: Re: Cinematica del manovellismo di spinta rotativo  | |
| |
|   | | | | Cinematica del manovellismo di spinta rotativo |  |
|
Argomenti simili |  |
|
| | Permessi in questa sezione del forum: | Non puoi rispondere agli argomenti in questo forum.
| |
| |
| |
