| | Esercizio sul doppio pendolo |  |
|
+3nicola.d.angelo91 Italo Pluchino vdr88 7 partecipanti |
| Autore | Messaggio |
|---|
vdr88
Numero di messaggi : 7
Corso di appartenenza : Dinamica e Controllo dei Sistemi Meccanici
NomeCognome : Vincenzo Di Rubba
Data d'iscrizione : 24.10.11
 |  Titolo: Esercizio sul doppio pendolo Titolo: Esercizio sul doppio pendolo  Mer Feb 01, 2012 3:04 pm Mer Feb 01, 2012 3:04 pm | |
| Salve a tutti! Siamo ancora Di Rubba e Marrone, abbiamo svolto un nuovo esercizio con opportune spiegazioni, di cio' che e' stato fatto, e speriamo in modo corretto. Mancano i passaggi matematici perchè sarebbe stato troppo lungo scriverlo in equazioni al pc .Nel caso qualcuno ne avesse bisogno possiamo sempre farne una scansione e linkarveli. Ci sono alcuni dubbi sulla seconda parte dell'esercizio e quale posto migliore se non il forum per chiedere aiuto. Speriamo di aver fatto cosa gradita. Saluti!  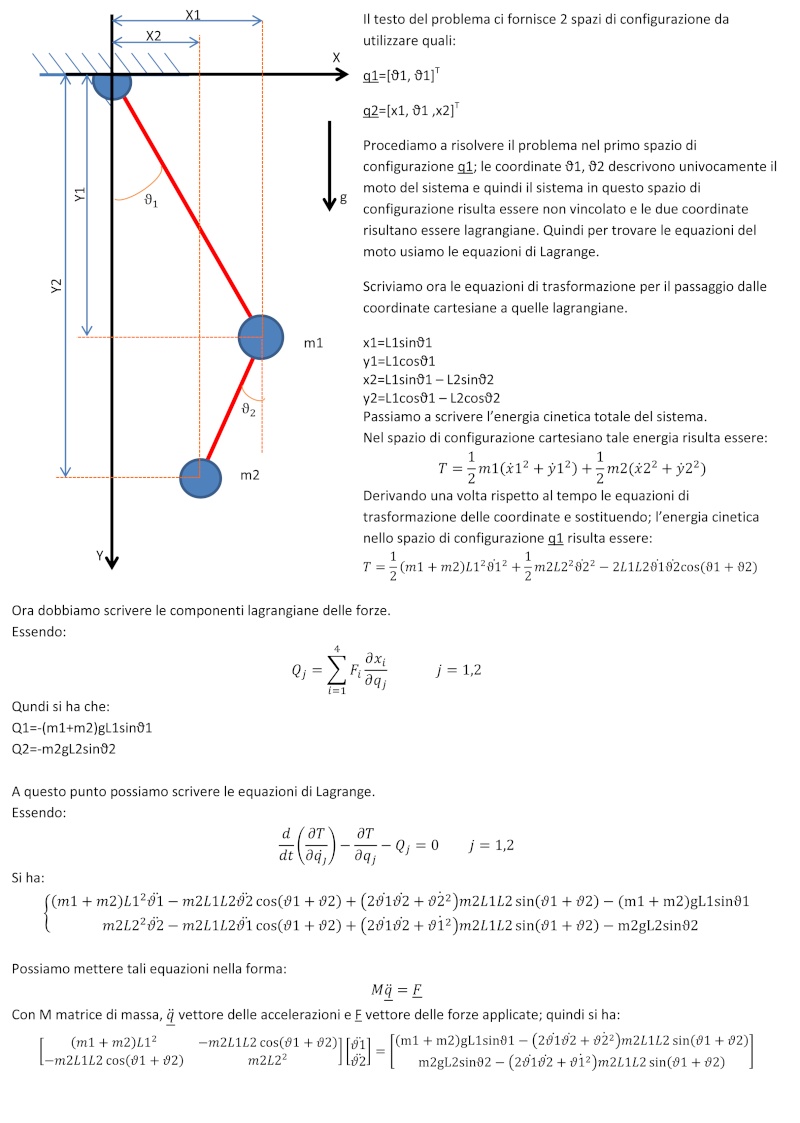  | |
|
  | |
Italo Pluchino
Numero di messaggi : 4
Corso di appartenenza : Dinamica e Controllo dei Sistemi Meccanici
NomeCognome : Italo Pluchino
Data d'iscrizione : 11.10.11
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Mer Feb 01, 2012 3:49 pm Mer Feb 01, 2012 3:49 pm | |
| Ciao ragazzi, per quel che riguarda la prima parte dell'esercizio, credo che abbiate sbagliato l' ultima equazione di trasformazione, dovrebbe essere y2= L1cos(theta1)+L2cos(theta2).
Mentre nella seconda parte, stando anche a quello che avete scritto, si dovrebbero avere 3 equazioni di trasformazione e una di vincolo che leghi 2 coordinate...
Quindi nel sistema di 4 equazioni, le prime 3 sono di trasformazione e l'ultima di vincolo?
Ultima modifica di Italo Pluchino il Mer Feb 01, 2012 4:13 pm - modificato 2 volte. | |
|
  | |
vdr88
Numero di messaggi : 7
Corso di appartenenza : Dinamica e Controllo dei Sistemi Meccanici
NomeCognome : Vincenzo Di Rubba
Data d'iscrizione : 24.10.11
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Mer Feb 01, 2012 3:53 pm Mer Feb 01, 2012 3:53 pm | |
| Ciao Italo riguardo al primo punto hai ragione, è stato un'errore di battitura; riguardo al secondo però sono sempre 4 le equazioni di trasformazione in quanto le coordinate cartesiane sone sempre x=[x1, y1, x2, y2] | |
|
  | |
Italo Pluchino
Numero di messaggi : 4
Corso di appartenenza : Dinamica e Controllo dei Sistemi Meccanici
NomeCognome : Italo Pluchino
Data d'iscrizione : 11.10.11
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Mer Feb 01, 2012 4:10 pm Mer Feb 01, 2012 4:10 pm | |
| Scusatemi avete ragione, per scrivere l' equazione dell'energia cinetica
si ha bisogno delle 4 equazioni di trasformazione.
A questo punto però va scritta l'equazione di vincolo, x1=L1sin(theta1) ad esempio.
Adesso mi domando come proseguirà l'esercizio, ammesso che sia valido proseguire come nella prima parte (e dato per scontato che il procedimento sia corretto), si arriverà alla determinazione del vettore q due punti, però andrà utilizzata anche l'equazione di vincolo; avrei un'idea sul come procedere, ma non vorrei scrivere sciocchezze.
Per questo aspetto conferme dal professore De Falco prima di andare oltre.
A presto. | |
|
  | |
ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Mer Feb 01, 2012 6:11 pm Mer Feb 01, 2012 6:11 pm | |
| molto bene questa discussione. Mi sembra emerga una questione seria.
Che differenza c'è tra equazioni di vincolo (olonomo) ed equazioni di trasformazione ?
Innanzitutto credo che la questione diventi immediatamente più chiara se parliamo di: equazioni di trasformazione delle coordinate.
- Comunque, le
equazioni di vincolo (olonomo) sono le relazioni tra le coordinate che definiscono lo spazio di configurazione del modello ovvero le relazioni tra le componenti del vettore x . - Le equazioni di trasformazione delle coordinate sono relazioni con cui si trasforma il vettore x in un altro vettore di coordinate, ad esempio q
| |
|
  | |
nicola.d.angelo91
Numero di messaggi : 28
Corso di appartenenza : Dinamica e Controllo dei Sistemi Meccanici
NomeCognome : Nicola D'Angelo
Data d'iscrizione : 28.03.11
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Gio Giu 05, 2014 4:24 pm Gio Giu 05, 2014 4:24 pm | |
| Salve ragazzi cercando di rifare l'esercizio del "doppio pendolo" non ho potuto fare a meno di notare che c'è un errore nelle equazioni di vincolo dato che l'angolo nella traccia è -Teta2 e non Teta2 quindi le equazioni di vincolo diventano x2=L1 sen Θ1 + L2 Sen Θ2 (che in caso di angolo negativo come nel disegno diventa L1 senΘ1-L2senΘ2) così anche per y2 e tutto quello che ne deriva.... Per quanto riguarda poi il punto b) dell'esercizio credo che non sia possibile risolverlo dato che le coordinate generalizzate scelte per descrivere il sistema anche se in numero superiore a quelle minime (2) non bastano a indicare una posizione univoca del sistema. ( x1 Θ1 Θ2 andrebbe bene mentre x1 Θ1 x2 NO). Infatti nello scrivere l'equazione dell'energia cinetica per tale sistema solo in funzione delle tre coordinate x1 Θ1 x2 compare per forza anche un'altra coordinata che non riesco a esplicitare in funzione delle altre tre.  Cosa ne pensate? | |
|
  | |
Lu92Ta
Numero di messaggi : 18
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Luca Tamburrino
Data d'iscrizione : 25.02.15
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Mar Gen 12, 2016 8:11 pm Mar Gen 12, 2016 8:11 pm | |
| [img]  [/img] Questa può essere una risoluzione del continuo dell'esercizio | |
|
  | |
Anna di Pasqua
Numero di messaggi : 11
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Anna di Pasqua
Data d'iscrizione : 10.02.14
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Ven Gen 15, 2016 7:15 pm Ven Gen 15, 2016 7:15 pm | |
| Salve ragazzi, per la seconda parte del problema, dove le coordinate dello spazio di configurazione sono x1 Θ1 e x2, io ho utilizzato un'equazione di vincolo in cui compaiono le coordinate del vettore di configurazione, ovvero: (x2-x1)^2+((sqrt(L2^2-x2^2)-L1cosΘ1)^2= L2^2.
Per quanto riguarda le equazioni di trasformazioni ho posto:
x1=x1
y1=L1cosΘ1
x2=x2
y2=sqrt(L2^2-x2^2)+L1cosΘ1
Queste potrebbero essere esatte, poiche' ho cercato di scrivere sia l'equazione di vincolo sia le equazioni di trasformazioni utilzzando le coordinate a disposizione.
| |
|
  | |
Lu92Ta
Numero di messaggi : 18
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Luca Tamburrino
Data d'iscrizione : 25.02.15
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Ven Gen 15, 2016 7:25 pm Ven Gen 15, 2016 7:25 pm | |
| Anna le equazioni di trasformazione mi trovo con te tranne che per l'ultima, che dovrebbe essere y2=sqrt(L2^2-(x1-x2)^2)+L1cosΘ1
| |
|
  | |
Anna di Pasqua
Numero di messaggi : 11
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Anna di Pasqua
Data d'iscrizione : 10.02.14
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Sab Gen 16, 2016 6:46 am Sab Gen 16, 2016 6:46 am | |
| Luca si hai ragione, pensandoci è così...grazie mille | |
|
  | |
ddefalco
Admin

Numero di messaggi : 172
Località : Napoli
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Domenico de Falco
Data d'iscrizione : 29.12.08
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Sab Gen 16, 2016 10:33 am Sab Gen 16, 2016 10:33 am | |
| ah benissimo vedo che avete fatto proprio come pensavo.Ineffetti i listati matlab potete condividerli proprio cosi mettendoli nel corpo del messaggio del forum.
Mi fa molto piacere quest'uso del forum, era ora !!! | |
|
  | |
onoranto
Numero di messaggi : 8
Corso di appartenenza : Meccanica Applicata alle Macchine
NomeCognome : Antonio Onorato
Data d'iscrizione : 03.05.14
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  Lun Gen 18, 2016 5:54 pm Lun Gen 18, 2016 5:54 pm | |
| Ho provato anche io a risolvere questo esercizio sul doppio pendolo e mi trovo con lo svolgimento che avete proposto  | |
|
  | |
Contenuto sponsorizzato
 |  Titolo: Re: Esercizio sul doppio pendolo Titolo: Re: Esercizio sul doppio pendolo  | |
| |
|
  | |
| | Esercizio sul doppio pendolo |  |
|
