Diagramma velocità cesoia a ghigliottina

Salve a tutti.
Ho tovato dei problemi riguardo la rappresentazione grafica delle velocità dei punti P2 e P3 riguardante l'esercizio della cesoia a ghigliottina.
grazie in anticipi per eventuali chiarimenti

Ciao, ho provato a risolvere l'esercizio e questo è il risultato.
Il punto geometrico P in figura è rappresentativo dei punti fisici P1 e P2 appartenenti rispettivamente al corpo rigido BC e DC.
Quindi la configurazione rappresentata è quella dell'istante di taglio, in cui i punti P1 e P2 si trovano nella stessa posizione.
Per quanto riguarda il diagramma di velocità, essendo la cesoia a ghigliottina schematizzabile come un quadrilatero articolato, essa avrà sicuramente un grado di libertà e quindi possiamo assegnare la velocità di un elemento e ricavare le velocità di ogni punto. Assegnata la velocità dell'elemento BA, che è ovviamente una manovella, possiamo cominciare a disegnare il segmento rappresentativo di questa velocità che nella configurazione data è un segmento verticale (che in questo caso ha origine in A, che ovviamente ha velocità nulla come D).
Per ricavare la velocità di C, che è un punto comune sia alla biella (BC) che al bilanciere (CD). Poichè C appartiene a BC tracciamo un segmento ortogonale al segmento BC e che parte dall'estremo del segmento rappresentativo della velocità di B. Questo segmento intersecherà un altro segmento che parte da A ed è ortogonale a CD. L'intersezione di questi due segmenti è il punto rappresentativo della velocità del punto C.
Per quanto riguarda il punto P1 che è solidale al corpo rigido BC, la sua velocità è vP1=vB+(B-P1)xw in quanto solidale a B, e vP1=vC+(C-P1)xw in quanto solidale a C. A questo punto possiamo trovare il punto rappresentativo della velocità del punto P1, infatti questo sarà l'intersezione tra il segmento di origine VB e ortogonale al segmento BP ed il segmento di origine VC e ortognale a CP. Procedimento analogo vale per la velocità del punto P2, che è solidale sia al punto D che al punto C.

Ti ringrazio per la risposta.

Ciao, quindi la velocità di vP2 dovrebbe essere vP2=vC+(C-P2)xW che è la velocità di P2 solidale a C (che abbiamo già tracciato prima), e vP2=vD+(D-P2)xW in quanto solidale a D.
Quindi graficamente, utilizziamo il segmento già tracciato in precedenza, ovvero il segmento che ha origine in VC e ortogonale a CP, poi basterà tracciare il segmento ortogonale a PD in A.
Supposto che A coincida con D.
Spero di aver intuito il resto della soluzione.
Ciao.

si, giusto, dove A coincide con D poichè rappresentativi di punti a velocità nulli in quanto solidali entrambi al telaio

Scusate ragazzi nel caso in cui dovessimo disegnare il diagramma delle accelerazioni?
come si dovrebbe operare

Vi ringrazio anticipatamente.

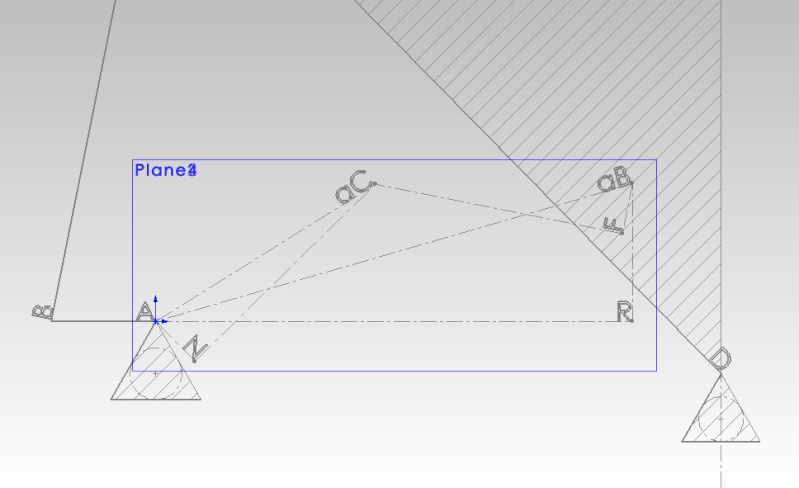Questo è un primo diagramma per i punti B e i punti C, in seguito provo a trovare le accelerazioni per i punti P1 e P2.
Essendo un meccanismo, esso ha un grado di libertà, quindi possiamo assegnare arbitrariamente l'accelerazione angolare di uno dei quattro elementi rigidi (io ho scelto l'accelerazione angolare del corpo rigido AB). Per trovare l'accelerazione del punto B basta sommare i due vettori w^2(A-B) e il vettore (A-B)xw'a (dove w'a è proprio l'accelerazione angolare di AB). Ovviamente w è noto perchè l'abbiamo trovato o assegnato precedentemente nel diagramma di velocità. Ovviamente il primo vettore è l'accelerazione centripeta che quindi sarà rivolta versa destra. Per quanto riguarda l'altro vettore ovviamente possiamo scegliere arbitrariamente il verso (nel mio caso concorde con la velocità angolare, quindi una "vera" accelerazione, in caso contrario avremo avuto una decelerazione). Da notare anche che è indifferente l'ordine con cui si disegnano i vettori, tanto la loro somma sarà sempre la stessa che ho indicato con il segmento aB.
Per trovare il punto rappresentativo dell'accelerazione di C possiamo sfruttare due relazioni: aC=aB+(wBC)^2(B-C)+(B-C)xw'BC e aC=wc^2(D-C)+(D-C)xw'c dove wBC è la velocità angolare di BC (nota dal diagramma di velocità), w'BC è l'accelerazione angolare di BC (che conosciamo solo in direzione e verso, ortogonale a (wBC)^2(B-C)), wc è la velocità angolare del corpo DC nota dal precedente diagramma di velocità ed infine (D-C)xw'c che anche in questo caso conosciamo in verso e direzione.
L'intersezione dei vettori su descritti ci fornisce il vettore rappresentativo dell'accelerazione del punto C.
Ovviamente le lunghezze usate nel disegno sono orientative, ma molto vicine a quelle effettive.

il procedimento è sempre lo stesso. Sfruttando le seguenti relazioni:
per il punto P2 solidale a DC vale aP2=wd^2(D-P2)+(D-P2)xw'd, dove w'd è l'accelerazione angolare di DC.
per il punto P1 valgono: aP1=aB+wBC^2(B-P1)+(B-P1)xw'BC in quanto solidale a B e aP1=aC+wBC^2(C-P1)+(C-P1)xw'BC

Ok grazie, credo di aver capito.....sei stato davvero molto gentile.